Game Theory in Rock Paper Scissors

Game Theory in Rock Paper Scissors.

Game theory is a mathematical framework for analyzing cooperation and conflict. Early work was motivated by recreational and gambling games such as chess, hence the “game” in game theory. But it quickly became clear that the framework had much broader application. Today, game theory is used for mathematical modeling in a wide range of disciplines, including many of the social sciences, computer science, and evolutionary biology. In my notes, | draw examples mainly from economics.

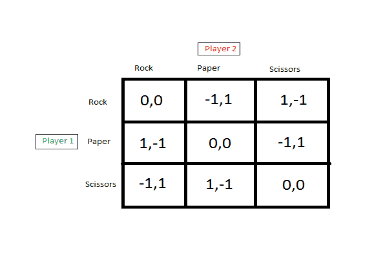
An example: Rock-Paper-Scissors. The game Rock-Paper-Scissors (RPS) is represented in Figure 1 in what is called a game box. There are two players, 1 and 2. Each player has three strategies in the game:

R

P

R

0, 0

-1, 1

1, -1

P

-1,1

0, 0

-1, 1

S

-1, 1

1, -1

0, 0

Figure 1: A game box for Rock-Paper-Scissors (RPS).

R (rock), P (paper), and S (scissors). Player 1 is represented by the rows while player 2 is represented by the columns.

If player 1 chooses R and player 2 chooses P then this is represented as the pair, called a strategy profile, (R,P) and the result is that player 1 gets a payoff of -1 and player 2 gets a payoff of +1, represented as a payoff profile (-1, 1). For interpretation, think of payoffs as encoding preferences over winning, losing, or tying, with the understanding that S beats P (because scissors cut paper), P beats R (because paper can wrap a rock… ), and R beats S (because a rock can smash scissors). If both choose the same, then they tie. The interpretation of payoffs is actually quite delicate and | discuss this issue at length in Section 3.3. This game is called zero-sum because, for any strategy profile, the sum of payoffs is zero. In any zero-sum game, there is a number V , called the value of the game, 2 with the property that player 1 can guarantee that she gets at least V no matter what player 2 does and conversely player 2 can get -V no matter what player 1 does. | provide a proof of this theorem in Section 4.5. In this particular game, V = 0 and both players can guarantee that they get 0 by randomizing evenly over the three strategies. Note that randomization is necessary to guarantee a payoff of at least 0. In Season 4 Episode 16 of the Simpsons, Bart persistently plays Rock against Lisa, and Lisa plays Paper, and wins. Bart here doesn’t even seem to understand the game box, since he says, “Good old rock. Nothing beats that.”

What is the Nash Equilibrium?

The Nash Equilibrium is a concept of game theory where the optimal outcome of a game is one where no player has an incentive to deviate from his chosen strategy after considering an opponent’s choice. Overall, an individual can receive no incremental benefit from changing actions, assuming other players remain constant in their strategies. A game may have multiple Nash Equilibria or none at all.

The Nash Equilibrium is the solution to a game in which two or more players have a strategy, and with each participant considering an opponent’s choice, he has no incentive, nothing to gain, by switching his strategy. In the Nash Equilibrium, each player’s strategy is optimal when considering the decisions of other players. Every player wins because everyone gets the outcome they desire. To quickly test if the Nash equilibrium exists, reveal each player’s strategy to the other players. If no one changes’ his strategy, then the Nash – Equilibrium is proven.

For example, imagine a game between Tom and Sam. In this simple game, both players can choose strategy A, to receive $1, or strategy B, to lose $1. Logically, both players choose strategy A and receive a payoff of $1. If you revealed Sam’s strategy to Tom and vice versa, you see that no player deviates from the original choice. Knowing the other player’s move means little and doesn’t change either player’s behavior. The outcome A, A represents a Nash Equilibrium.

Pure-Strategy Nash Equilibrium Rational players think about actions that the other players might take. In other words, players form beliefs about one another’s behavior. For example, in the BoS game, if the man believed the woman would go to the ballet, it would be prudent for him to go to the ballet as well. Conversely, if he believed that the woman would go to the fight, it is probably best if he went to the fight as well. So, to maximize his payoff, he would select the strategy that yields the greatest expected payoff given his belief. Such a strategy is called a best response (or best reply).

Suppose player i has some belief s—i € S-i about the strategies played by the other players. Player i’s strategy si € Si is a best response if ui (si, s-i) = ui (s i, s—i) for every si € Si.

We now define the best response correspondence), BRi (s-i), as the set of best responses player i has to s-i. It is important to note that the best response correspondence is setvalued. That is, there may be more than one best response for any given belief of player i. If the other players stick to s-i, then player i can do no better than using any of the strategies in the set BRi (s-i).

In the BoS game, the set consists of a single member:

BRm (F) = {F} and BRm (B) = {B}.

Thus, here the players have a single optimal strategy for every belief.

In this game, BR1 (L) = {M}, BR1(C) = {U,M}, and BR1(R) = {U}.

Also, BR2(U) = {C,R}, BR2(M) = {R}, and BR2(D) = {C}.

You should get used to thinking of the best response correspondence as a set of strategies, one for each combination of the other players’ strategies. (This is why we enclose the values of the correspondence in braces even when there is only one element.)

Player 2

L

C

R

U

2, 2

1, 4

4, 4

M

3, 3

1, 0

1, 5

D

1, 1

0, 5

2, 3

Player 1

Figure 2: The Best Response Game.

We can now use the concept of best responses to define Nash equilibrium: a Nash equilibrium is a strategy profile such that each player’s strategy is a best response to the other players’ strategies:

The strategy profile (s* i, s* -i) € Sis a pure-strategy Nash equilibrium if, and only if s* i € BRi(s*-i) for each player i € |. An equivalent useful way of defining Nash equilibrium is in terms of the payoffs players receive from various strategy profiles.

Rock Paper Scissors and Game Theory

On the count of three and the verbal command “shoot”, each player simultaneously forms his hand into the shape of either a rock, a piece of paper, or a pair of scissors. If both pick the same shape, the game ends in a tie. Otherwise, one player wins and the other loses according to the following rule: rock beats scissors, scissors beats paper, and paper beats rock. Each obtains a payoff of 1 if he wins, -1 if he loses, and 0 if he ties.

Rock, Paper, Scissors

It is immediately obvious that this game has no Nash equilibrium in pure strategies: The player who loses or ties can always switch to another strategy and win. This game is symmetric, and we shall look for symmetric mixed strategy equilibria first. Let p, q, and 1 – p – q be the probability that a player chooses R, P, and S respectively. We first argue that we must look only at completely mixed strategies (that is, mixed strategies that put a positive probability on every available pure strategy). Suppose not, so p1 = 0 in some (possibly asymmetric) MSNE. If player 1 never chooses R, then playing P is strictly dominated by S for player 2, so she will play either R or S. However, if player 2 never chooses P, then S is strictly dominated by R for player 1, so player 1 will choose either R or P in equilibrium. However, since player 1 never chooses R, it follows that he must choose P with probability 1. But in this case player 2’s optimal strategy will be to play S, to which either R or S are better choices than P. Therefore, p1 = 0 cannot occur in equilibrium. Similar arguments establish that in any equilibrium, any strategy must be completely mixed. We now look for a symmetric equilibrium. Player 1’s payoff from R is p(O) + q(-1) + (1 – p -q)(1) = 1-p -2q. His payoff from P is 2p +q -1. His payoff from S is q -p. In an MSNE, the payoffs from all threepure strategies must be the same, so:

1-p-2q=2pt+q-1=q-p

Solving these equalities yields p = q = 1/3.

Whenever player 2 plays the three pure strategies with equal probability, player 1 is indifferent between his pure strategies, and hence can play any mixture. In particular, he can play the same mixture as player 2, which would leave player 2 indifferent among his pure strategies. This verifies the first condition in Proposition 1. Because these strategies are completely mixed, we are done. Each player’s strategy in the symmetric Nash equilibrium is (1/3, 1/3, 1/3). That is, each player chooses among his three actions with equal probabilities. Is this the only MSNE? We already know that any mixed strategy profile must consist only of completely mixed strategies in equilibrium. Arguing in a way similar to that for the pure strategies, we can show that there can be no equilibrium in which players put different weights on their pure strategies. You should check for MSNE in all combinations. That is, you should check whether there are equilibria, in which one player chooses a pure strategy and the other mixes; equilibria, in which both mix; and equilibria in which neither mixes. Note that the mixtures need not be over the entire strategy spaces, which means you should check every possible subset. Thus, in a 2×2 two-player game, each player has three possible choices: two in pure strategies and one that mixes between them. This yields 9 total combinations to check. Similarly, in a 3 x 3 two-player game, each player has 7 choices: three pure strategies, one completely mixed, and three partially mixed. This means that we must examine 49 combinations! (You can see how this can quickly get out of hand.) Note that in this case, you must check both conditions of Proposition 1.

We have established that Rock Paper Scissors does not have a dominant strategy for either of the players. How do you use that information to incur that there is no Nash equilibrium? Quite simple! If Player 2’s strategy is Rock, Player 1 should choose Paper, but if Player 1 chooses Paper, it is profitable for Player 2 to deviate and choose Scissors instead. When player 2 chooses Scissors, Player 1 would want to deviate and choose Rock, and so forth. Thus, we can see that there is no Nash Equilibrium for this game owing to the cyclical manner of the game.